What Are Integers? Your Simple Guide To These Core Math Numbers

Have you ever stopped to think about the numbers we use every single day? It's almost like we just pick them up and go, not giving much thought to their true nature. Yet, some numbers, like integers, form a very basic building block for so much of what we do in math and even in our daily routines. So, what exactly are these numbers that show up everywhere?

We often deal with things that are whole or complete, like counting a group of friends or figuring out how many apples are in a basket. But what happens when we need to talk about things that are less than zero, or perhaps a number that isn't a piece of something? This is where the idea of integers comes into play, providing a way to describe these specific quantities.

Today, as of late 2023, we're going to explore what integers are all about, drawing insights from foundational math concepts. We'll look at their characteristics, see how they fit into the bigger picture of numbers, and even touch on why they're quite important in various situations, you know, in the world around us.

• Pug And Pug
• Names For Grandma
• Shanin Blake Leaked
• Oregon Renaissance Faire
• Brooke Monk Nudes

Table of Contents

• What Exactly Are Integers?
  • The Origin of the Word
• The Parts of Integers
  • Positive Integers
  • Negative Integers
  • Zero: The Middle Point
• Integers on a Number Line
• How Integers Relate to Other Numbers
  • Integers and Whole Numbers
  • Integers and Natural Numbers
  • What Integers Are Not
• Why Integers Matter in Real Life
• Working with Integers: A Quick Look
• Frequently Asked Questions About Integers

What Exactly Are Integers?

When we talk about numbers in mathematics, a big group of them are called integers. My text points out that "Integers are a fundamental concept in mathematics, representing a set of whole numbers that includes both positive and negative numbers, along with zero." This means they are a collection that covers quite a bit of ground, you know, in the number world.

Basically, an integer is any number that does not have a fractional part or a decimal part. My text also says, "In math, the integers are numbers that do not contains fractions or decimals." This is a key feature that helps us tell them apart from other types of numbers, like those you might see when measuring something very precise.

They are, in a way, complete numbers. My text mentions, "By integer, we understand a number without any decimal or fractional part." So, if you're counting items, or perhaps tracking scores, you're very likely dealing with integers, as they show up in many simple counting situations.

• Dee Dee Davis
• Haircuts For Men
• Megumi Summoning Mahoraga
• Pastel Goth Dti
• Sabrina Carpenter Naked

The set of integers is quite extensive. My text explains that "Integers are a set of numbers that include all whole numbers (zero and positive numbers) as well as negative numbers." This broad inclusion makes them incredibly useful for describing quantities that go both above and below a starting point, like zero.

They are, in some respects, discrete points. My text notes, "Integers can be thought of as discrete, equally spaced points on an infinitely long number line." This visual helps us picture them as distinct marks, not continuous stretches, which is a big part of their character.

The Origin of the Word

The name "integer" itself gives us a clue about what these numbers are. My text tells us that "'integer' is a latin word which means 'whole' or 'intact'." This origin highlights their nature as complete units, without any pieces missing or added on, so to speak.

This Latin root really helps to reinforce the idea that integers are not broken up. It means they do not include fractions or decimals, as my text further clarifies. So, when you hear the word, you can instantly think of something that is entire.

The Parts of Integers

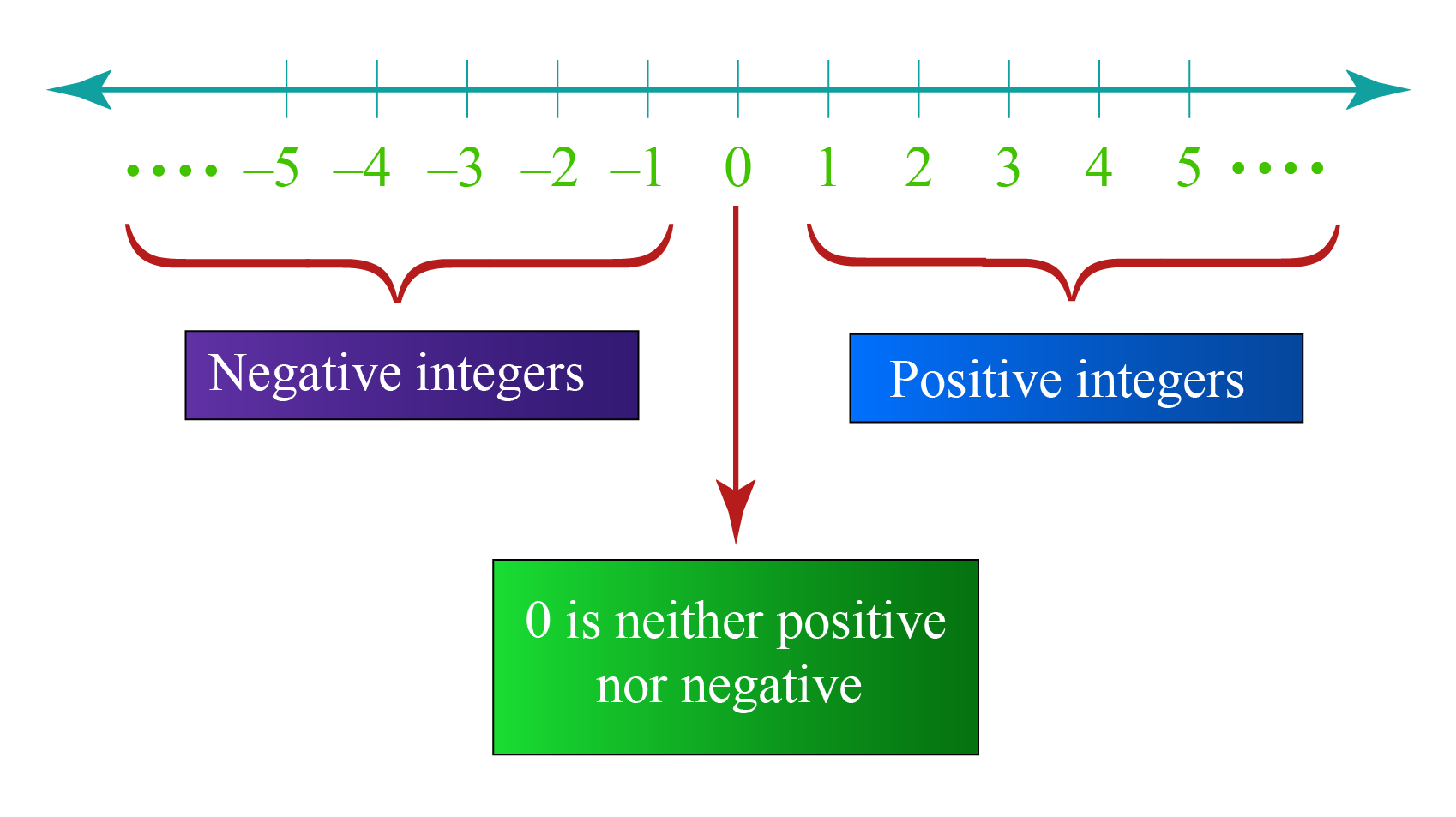
Integers are not just one type of number; they are a group made up of three distinct kinds. My text states, "They can be positive, negative, or zero." This division helps us categorize them and use them accurately in different situations, like when talking about temperature.

Understanding these different parts is quite important for working with integers. It allows us to properly represent various quantities, whether they are above a certain point or below it, or right at the starting line, basically.

Positive Integers

Positive integers are the numbers we use for counting things, like one, two, three, and so on. My text refers to these as "natural numbers (counting numbers)." They are the numbers that are greater than zero, and they keep going up indefinitely.

When you add items to a group, you are using positive integers. For example, if you have two apples and then get three more, you're working with these kinds of numbers. They represent an increase or a gain, typically.

Negative Integers

Negative integers are numbers that are less than zero. They are represented with a minus sign in front of them, like -1, -2, -3, and so on. My text includes these as part of the integer set, saying "Integers include all whole numbers and negative numbers."

These numbers are very useful for showing a decrease or a loss. For instance, if the temperature drops below zero, or if you owe someone money, you would use negative integers to describe that situation, you know, to show the amount.

My text also mentions that the set of integers includes the "additive inverses" of natural numbers. This means that for every positive counting number, there's a corresponding negative number that, when added together, gives you zero. For example, the inverse of 5 is -5.

Zero: The Middle Point

Zero is a special integer. It is neither positive nor negative. My text clearly states that integers include "zero." It acts as the central point on a number line, separating the positive numbers from the negative numbers, which is pretty neat.

Zero can represent the absence of something, or a starting point. If you have no items, you have zero. If you are at ground level, your elevation is zero. It's a very important reference point in mathematics, too it's almost a pivot.

Integers on a Number Line

One of the best ways to picture integers is on a number line. My text explains, "Integers can be thought of as discrete, equally spaced points on an infinitely long number line." This visual tool helps us see their order and relationship to one another.

On a number line, zero is right in the middle. Positive integers stretch out to the right, getting larger as you move further away from zero. Negative integers stretch out to the left, getting smaller as you move further from zero, which is really quite intuitive.

Using a number line can help us understand how integers relate to each other in terms of size and position. It's a good way to visualize operations like addition and subtraction with these numbers, too it's very helpful for learning.

How Integers Relate to Other Numbers

It's helpful to know how integers fit in with other kinds of numbers we use. My text gives us some good clues about this. They are a specific category, and they have clear boundaries, so to speak, that define them.

Integers and Whole Numbers

Whole numbers are a group that includes zero and all the positive counting numbers (0, 1, 2, 3, ...). My text notes that "Integers include all whole numbers and negative numbers." This means that every whole number is also an integer, but not every integer is a whole number.

The main difference, obviously, is the presence of negative numbers within the integer set. Whole numbers simply do not go below zero, whereas integers do. This distinction is quite important when you are trying to classify numbers correctly.

Integers and Natural Numbers

Natural numbers, sometimes called counting numbers, are 1, 2, 3, and so on. Some definitions include zero in natural numbers, but often it starts from 1. My text says "The set includes zero, the natural numbers (counting numbers), and their additive inverses." So, natural numbers are a part of integers, too.

Just like with whole numbers, all natural numbers are integers. However, integers also include zero and all the negative numbers, which natural numbers do not. This makes integers a much broader collection of numbers, in a way.

What Integers Are Not

A very important aspect of integers is what they are not. My text makes this very clear: "Similar to whole numbers, integers also does not include the fractional part." This means you won't find numbers like 1/2 or 3/4 among integers.

My text also states, "It should be noted that an integer can never be a fraction, a decimal or a per cent." This is a defining characteristic. If a number has a part after a decimal point, or can be written as one number over another (a fraction), then it is not an integer.

So, numbers like 2.5, -0.75, or 1/3 are definitely not integers. They represent parts of a whole, or values between the distinct points on the number line that integers occupy. This distinction is pretty fundamental for how we categorize numbers.

Why Integers Matter in Real Life

Integers are not just abstract concepts for math class; they show up in our everyday lives in many ways. Understanding them helps us make sense of various situations, you know, the ones that come up all the time.

Think about temperature, for instance. When the weather report says it's -5 degrees Celsius, that's a negative integer telling you how cold it is below freezing. Or if it's 20 degrees, that's a positive integer. This is a very common application.

Money is another area where integers are constantly used. If you have $100 in your bank account, that's a positive integer. If you owe $20, that's represented as -20. This helps us keep track of financial situations, actually, quite precisely.

In sports, scores often involve integers. A football team might gain 10 yards (positive 10) or lose 5 yards (negative 5). Golf scores use positive numbers for strokes over par and negative numbers for strokes under par, which is a good example.

Elevations are also described using integers. Sea level is often considered zero. A mountain peak might be 5,000 feet above sea level (positive 5,000), while a valley might be 200 feet below sea level (negative 200). This helps us understand vertical positions, basically.

Even in computer science, integers are a fundamental data type. When computers count things or perform calculations without fractions, they are often using integers. This is a very basic building block for digital systems, too, it's really important.

These real-world examples, you know, highlight how integers provide a simple yet powerful way to represent whole amounts, including those that indicate a direction or position relative to a zero point. They are quite versatile tools for describing quantities.

To learn more about numbers and their different types, you can explore other resources on our site. There's a lot to discover beyond just integers, honestly, a whole lot.

Working with Integers: A Quick Look

While this post focuses on what integers are, it's good to know they can be used in basic math operations. You can add them, subtract them, multiply them, and divide them, just like other numbers. The rules for these operations are quite consistent.

For example, adding a positive integer moves you to the right on a number line, while adding a negative integer (or subtracting a positive one) moves you to the left. These movements help us visualize the outcomes of calculations, you know, to see what happens.

My text mentions, "The integers are generated from the set of counting numbers 1, 2, 3,… and the operation of subtraction." This points to how subtraction, especially, helps create the full set of integers by allowing us to go below zero. This is a pretty neat concept, too.

Understanding these basic operations is a next step once you grasp what integers are. They are the foundation for more complex mathematical ideas and problems, obviously, in many areas of study.

For more detailed explanations and practice, you can find many resources online, like this helpful guide on Khan Academy, which covers the basics of integers and their uses. It's a good place to start, actually.

You can also find more information about various mathematical concepts on our site, which might help you build a broader picture of how numbers work. There are many connections between different areas of math.

Frequently Asked Questions About Integers

Are fractions integers?

No, fractions are not integers. My text clearly states that integers "do not include the fractional part" and that "an integer can never be a fraction." Integers are whole numbers, meaning they do not have any parts or pieces, which is a key distinction.

Is zero an integer?

Yes, zero is definitely an integer. My text mentions that integers include "zero" and that "An integer is any number including 0, positive numbers, and negative numbers." Zero is a very important part of the integer set, acting as the central point.

What is the difference between whole numbers and integers?

The main difference is that integers include negative numbers, while whole numbers do not. Whole numbers start at zero and go up (0, 1, 2, 3, ...), but integers include those whole numbers plus all the negative whole numbers (-1, -2, -3, ...). So, all whole numbers are integers, but not all integers are whole numbers, basically.