Have you ever looked at a set of numbers and felt like you were only seeing part of the story? It's a common feeling, that. We often hear about the "average" or the "mean," and these are indeed helpful starting points. Yet, there's so much more to truly grasp what your data is trying to tell you, and this is where the idea of the "mean of sigma" comes into play. It's not a single, simple calculation, but rather a way to think about how two very important statistical ideas work hand in hand.
You see, when we measure something, like how long an event lasts or how tall plants grow, we get numbers. These numbers rarely stay exactly the same, do they? They usually have some differences among them. So, when we talk about a "mean," we are, in a way, measuring how much individual observations might stray from a true, constant value. It is, basically, a way to find a central point for all those numbers.
But what if those numbers are really spread out, or really close together? That central point, the mean, might not tell you everything you need to know. This is where "sigma," or standard deviation, enters the picture. It helps us understand the spread. Thinking about the "mean of sigma" helps us connect these two crucial ideas, giving us a much clearer view of the information we have in front of us. It is, actually, pretty neat how they fit together.
Table of Contents
- The Core Idea: What "Mean of Sigma" Really Points To
- Why Mean and Sigma Are a Dynamic Duo
- Real-World Glimpses: Using Mean and Sigma
- Common Questions About Mean and Sigma
- Bringing It All Together: Your Data's Narrative
The Core Idea: What "Mean of Sigma" Really Points To
When people talk about the "mean of sigma," they are not usually referring to a single, formal statistical calculation. Instead, they are often pointing to the very close relationship between the mean and the standard deviation. It is about how these two numbers, taken together, paint a full picture of your data. Think of it like this: the mean tells you where the center of your data is, and sigma tells you how much the data points typically spread out from that center. So, you know, they're like two sides of the same coin, pretty much.
Explaining Sigma (Standard Deviation)
Sigma, which is just another name for standard deviation, measures how spread out your numbers are from the average. It is, in a way, an average of how much each data point differs from the mean. My text mentions this, that you calculate the "sum of absolute deviations or the square root of the sum of squared deviations," and then "you average them to get the mean deviation and the standard deviation." So, in a very real sense, sigma itself is a kind of average, a measure of typical deviation. It gives you a sense of how much individual measurements usually vary from the central point, which is the mean. This is, honestly, a very important part of data analysis.
Consider a simple example: if you measure the height of a group of people, the mean might be 5 feet 8 inches. Now, if the standard deviation is small, say 1 inch, it means most people are very close to that 5 feet 8 inches mark. But if the standard deviation is large, like 6 inches, it tells you there is a much wider range of heights in that group. So, you know, the standard deviation is, basically, giving you a sense of consistency, or the lack of it, in your numbers. It helps you understand if your data points are clustered tightly or if they are scattered far and wide. It is, after all, a key indicator of data variability.
- Paige Spiranac Leaked
- Brooke Monk Nudes
- Sabu Retirement Match
- Moto Moto Madagascar
- Australia Spider Season
Mean vs. Average: A Clear View
My text also makes a rather interesting distinction between "mean" (均值) and "average" (平均值). It says "mean (均值) is the result obtained by averaging all values where measurements deviate from a constant true value; average (平均值) is the direct average of measured values in a series with internal differences." This is quite a thoughtful way to look at it, actually. It suggests that a "mean" is perhaps more about finding a central point when there is an underlying, perhaps ideal, true value that observations might drift from. It's like aiming for a bullseye, and the mean shows where your shots tend to land, even if they miss the exact center a little. So, in that case, the mean is a measure of central tendency for a set of observations that are, in some way, trying to hit a consistent mark.
On the other hand, the "average" might be seen as simply summing up a bunch of numbers that naturally vary and dividing by how many there are, without necessarily implying a "true" value they are all trying to reflect. For instance, if you are averaging the daily temperatures over a month, there is no single "true" temperature that every day is trying to be; each day has its own distinct temperature. The average just gives you a general idea of the temperature range for that month. So, you know, the distinction points to the purpose behind the calculation. The "mean of sigma" really focuses on how these two concepts, central point and spread, are always linked when we analyze data, particularly when we are looking for insights into measurements that might vary around some expected value. It is, basically, about understanding both the center and the typical amount of variation around it.
Why Mean and Sigma Are a Dynamic Duo
The mean and standard deviation work best when they are considered together. One without the other often tells an incomplete story. Imagine you are comparing two different ways of making a product. Both might have the same average quality score, but if one method has a much larger standard deviation, it means its quality is far less consistent. So, you know, it is not just about the typical outcome, but also about how much that outcome can jump around. This combination is, honestly, what makes them so powerful for data interpretation.
Seeing the Whole Picture
The mean gives you the central tendency, a kind of typical value for your data. But without the standard deviation, you have no idea how typical that "typical" value really is. Is it a tight cluster of data points around the mean, or are they scattered far and wide? The standard deviation provides that crucial context. It tells you about the spread, the variability, the dispersion of your data points. For example, if you have two groups of students, and both groups have an average test score of 75, but one group has a standard deviation of 5 points and the other has a standard deviation of 15 points, what does that tell you? The first group is more consistent, with most students scoring very close to 75. The second group, however, has students with a much wider range of scores, from very low to very high. So, you know, the mean alone would miss this really important difference in how the groups performed. It is, basically, about seeing the whole distribution, not just the middle.
This pairing of mean and standard deviation is particularly useful when you are trying to understand the characteristics of a group or a process. It helps you identify if there is a lot of variation that needs addressing, or if the process is pretty stable. For instance, in quality control, you would want a low standard deviation for product measurements, even if the mean is on target. A high standard deviation means inconsistent products, which is, obviously, not ideal. This combination, in a way, gives you a snapshot of both where things generally land and how much they wiggle around that landing spot. It is, frankly, pretty insightful for anyone looking at data.
When Sigma Tells a Story About the Mean
My text brings up an interesting point: "What does it imply for standard deviation being more than twice the mean?" This is a very specific scenario that usually suggests something quite striking about your data. For data that is strictly positive, like "timing data from event durations," if the standard deviation is significantly larger than the mean, it often means the data is very skewed. It is, in fact, not symmetrical at all. You might have a lot of small values and a few very large ones pulling the mean up, while the spread is huge. This kind of situation is, arguably, a big red flag that the mean might not be the best single summary of your data.
Consider timing data, for instance. If the average time for a task is 10 minutes, but the standard deviation is 25 minutes, that tells you there are likely many tasks that finish very quickly, and then a few that take an incredibly long time. The mean of 10 minutes, in this case, does not really represent a typical experience. This kind of relationship between mean and sigma, where sigma is much larger, often indicates that the data does not follow a nice, bell-shaped curve. It might be heavily concentrated at one end with a long tail stretching out. So, you know, when sigma is disproportionately large compared to the mean, it is a strong hint that you should look closer at the shape of your data's distribution. It is, pretty much, an alert to dig deeper into what is going on.
Real-World Glimpses: Using Mean and Sigma
Understanding the "mean of sigma" is not just for statisticians; it has practical applications across many fields. From analyzing survey results to assessing machine learning models, these two numbers are constantly giving us important clues. It is, honestly, about getting a handle on real-world numbers and what they mean for decisions. We see this in so many different areas, you know.
Understanding Data Spreads
Different distributions will have different characteristics when it comes to their mean and standard deviation, as my text hints at. For example, a dataset might be symmetrical, with most values clustering around the mean, creating a bell-like shape. Here, the mean is a good representation of the center, and the standard deviation tells you how wide that bell is. However, some data sets are skewed, meaning they have a longer tail on one side. Income data, for instance, is often skewed, with many people earning moderate incomes and a few earning very high incomes. In such cases, the mean can be pulled significantly by those extreme values, and the standard deviation will be large. So, you know, just seeing the mean and sigma helps you picture the overall shape of the data, which is pretty useful.
When data is skewed, sometimes other measures of central tendency, like the median, might be more informative than the mean. My text brings up the idea of "pricing houses" and using the median instead of the mean for model performance. This is a perfect example. House prices are often skewed because of a few very expensive properties. If you just look at the mean house price, it might give a misleading idea of what a typical house costs in an area. The median, which is the middle value when all prices are lined up, is less affected by those extreme high prices. So, you know, understanding the mean and sigma, and how they relate to the shape of the data, helps you choose the best way to describe your numbers. It is, basically, about picking the right tool for the job.
Making Sense of Predictions
In the world of prediction and forecasting, understanding the "mean of sigma" is also very important. When you build a model to predict something, like a score from 0 to 100, you will have prediction errors. My text mentions interpreting "mape = 10" versus "mae = 10" in layman's words. These are measures of error. The mean of these errors might tell you if your model tends to over-predict or under-predict on average. But the standard deviation of these errors tells you how consistent your predictions are. Is your model usually off by a small, predictable amount, or are its errors wildly inconsistent? So, you know, the standard deviation of your prediction errors is a key indicator of your model's reliability.
A model with a low mean error but a high standard deviation of errors means that while it might be right on average, it is very unreliable for individual predictions. Conversely, a model with a slightly higher mean error but a very low standard deviation might be more trustworthy because its errors are consistent. This is, in fact, a very important distinction when deciding if a model is good enough for real-world use. The "mean of sigma" in this context helps you understand not just how much your predictions are off, but also how much that "off-ness" varies. It is, honestly, a deeper look into model quality. You can learn more about statistical modeling on our site, and link to this page for advanced data analysis techniques.
Common Questions About Mean and Sigma
People often have similar questions when they are first getting to grips with these concepts. Here are some common ones:
What does standard deviation tell you about the mean?
Well, the standard deviation tells you how much the individual data points typically spread out from the mean. If the standard deviation is small, it means the data points are generally very close to the mean, so the mean is a very good representation of the typical value. If it is large, the data points are more scattered, meaning the mean might not be as representative of every single data point. It is, basically, about how much variability there is around that central point.
Is standard deviation the average deviation?
Yes, in a way, it is. As my text suggests, when you calculate standard deviation, you are, in essence, averaging the deviations of each data point from the mean. It is not a simple arithmetic average of the raw deviations because of the squaring involved (to handle positive and negative deviations), but the result does represent a typical amount of deviation. So, you know, it gives you a single number that summarizes the average spread.
How do mean and standard deviation describe data?
Together, the mean and standard deviation give you a pretty good summary of a dataset. The mean tells you where the center of the data lies, providing a central value. The standard deviation tells you how spread out the data points are from that center. So, you know, they describe both the location and the dispersion of your data. For many common types of data distributions, these two numbers are often enough to get a very good feel for the entire set of numbers. You can find more detailed explanations on sites like Investopedia's page on Standard Deviation.
Bringing It All Together: Your Data's Narrative
Thinking about the "mean of sigma" is really about seeing the bigger picture in your numbers. It is not just about calculating a single average, but also about understanding how much your data points vary around that average. The mean gives you a central point, and the standard deviation tells you about the spread, or the typical deviation from that center. When sigma is much larger than the mean, especially for data that cannot be negative, it is a strong sign that your data might be very skewed, and the mean might not be the best single summary. So, you know, it is about getting a fuller sense of what your measurements are doing.
Understanding this relationship helps you make better sense of any set of numbers, whether you are looking at product quality, survey results, or the performance of a predictive model. It helps you ask better questions about what your data truly represents. So, next time you see a mean, do not forget to ask about its sigma. It will, basically, tell you so much more about the story your data is waiting to share with you.
Related Resources:


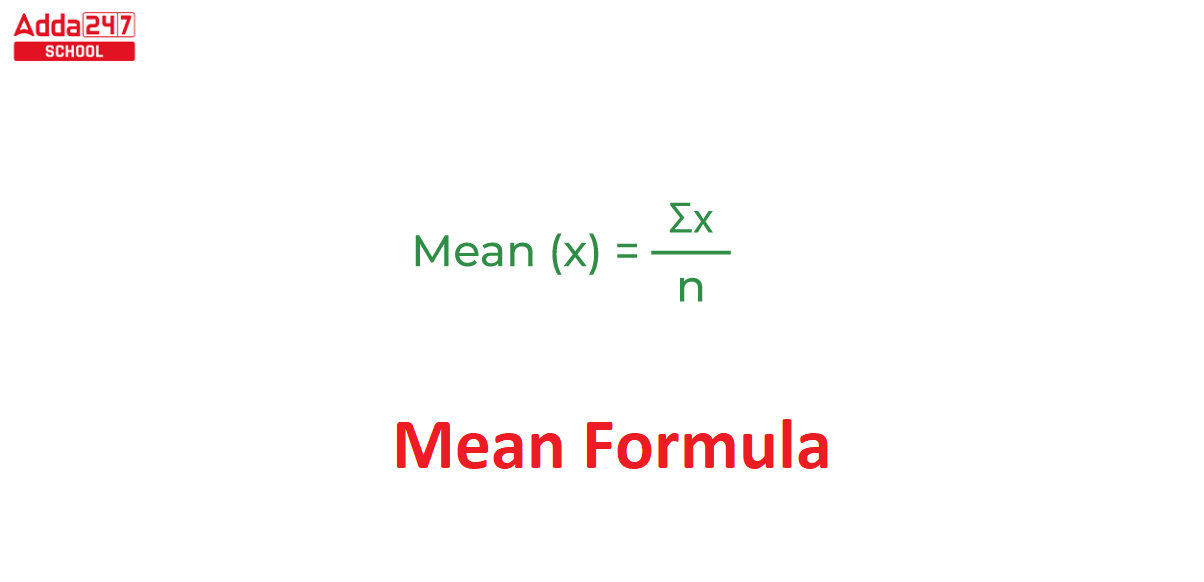
Detail Author:
- Name : Henderson Satterfield
- Username : gorczany.ollie
- Email : zora34@balistreri.net
- Birthdate : 1976-05-11
- Address : 139 Abernathy Plaza Suite 833 Port Theresia, MA 80749-3251
- Phone : 1-385-339-2201
- Company : Kessler-Heidenreich
- Job : Scientific Photographer
- Bio : Rerum repellat cum sit impedit velit dolorem assumenda. Dolorem et est ut dolorem beatae laborum. Odit voluptates delectus tenetur facilis id.
Socials
facebook:
- url : https://facebook.com/aurore.jerde
- username : aurore.jerde
- bio : Tempore harum voluptas exercitationem et id.
- followers : 4126
- following : 1376
linkedin:
- url : https://linkedin.com/in/aurore_dev
- username : aurore_dev
- bio : Eos ipsum eum odit nobis ratione.
- followers : 4871
- following : 989
instagram:
- url : https://instagram.com/aurorejerde
- username : aurorejerde
- bio : Quia unde laborum aut rerum ex eaque. Velit nemo nihil labore quis. Culpa odio possimus ea eius.
- followers : 1178
- following : 950